Qu'est-ce qu'une bonne isolation et quel est le lien avec la consommation d'énergie ?
Les matériaux isolants :
Les matériaux qui conduisent mal la chaleur sont appelés isolants. Ils sont généralement légers et remplis d’air immobile, ce qui empêche la chaleur de se propager facilement. Voici une liste des principaux isolants, classés en deux catégories :
Les isolants biosourcés :
Comme le chanvre, le lin, la fibre de bois, la ouate de cellulose, les balles de céréales, le coton recyclé, la paille de blé, le liège, et la laine de mouton.
Ces matériaux naturels sont renouvelables et ont un impact environnemental réduit.
Les isolants conventionnels :
Comme la laine de roche, la laine de verre, le polystyrène (expansé ou extrudé) et le polyuréthane.
Ces isolants synthétiques ou minéraux sont largement utilisés pour leurs performances et leur coût abordable.

Comment fonctionne un isolant ?
Pour qu’un matériau soit un bon isolant, il doit emprisonner de l’air et empêcher sa mise en mouvement. En effet, l’air est un excellent isolant thermique lorsqu’il est immobile. C’est pourquoi de nombreux isolants sont constitués de fibres ou de cellules qui retiennent l’air.
Cas n°1 : Matériau peu dense
Si l’isolant n’est pas assez dense, l’air peut circuler entre les fibres, créant des mouvements de convection. Ces mouvements facilitent la dissipation de la chaleur vers l’extérieur, réduisant l’efficacité de l’isolation.
Solution : Utiliser un isolant plus dense pour limiter la convection interne.
Cas n°2 : Matériau dense
Un isolant dense empêche l’air de bouger, éliminant ainsi les courants de convection interne. Cela rend l’isolation beaucoup plus efficace en conservant la chaleur à l’intérieur.
La performance des isolants :
La conductivité thermique (λ)
La performance d’un isolant est déterminée par sa conductivité thermique, notée λ (lambda), exprimée en watts par mètre-kelvin W/(m.K). Plus la valeur de λ est faible, plus le matériau est isolant.
Exemple : la laine de verre a un λ moyen de 0,036 W/m·K, et des isolants très performants comme la mousse de polyuréthane peuvent atteindre des valeurs λ = 0,023 W/(m·K).
La résistance thermique (R)
La résistance thermique notée R et exprimée en m².K/W mesure la capacité d’un isolant à résister au passage de la chaleur. Elle dépend de l’épaisseur de l’isolant (e) et de sa conductivité thermique (λ) :
La relation permettant de définir la résistance thermique d’une couche de matériau est définie par son épaisseur (en m) divisée par sa conductivité thermique (en W.(m.K)).
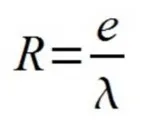
Exemple : Pour un panneau de laine de verre de conductivité thermique 0,035 W/(m.K) et d’épaisseur 18 cm, sa résistance thermique vaut :
R = 0,18/0,036 = 5,00 m².K/W
Coefficient de transmission thermique U
En France, on utilise aussi le coefficient de transmission thermique, noté U (en W/m²·K), qui est l’inverse de la résistance thermique :
U = 1/R
Par exemple une couche de matériau ayant une résistance thermique en partie courante R = 5 m²·K/W aura un coefficient de transmission thermique U = 0,20 W/(m²⋅K)
Du coefficient U à la consommation d'énergie :
Calcul de la puissance thermique nécessaire
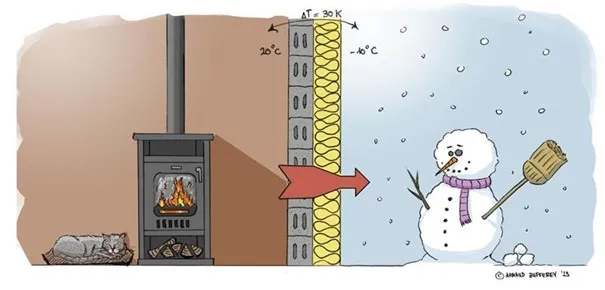
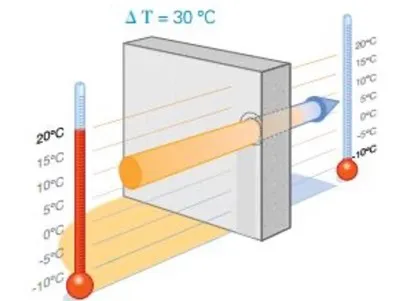
La différence de température entre l’intérieur et l’extérieur, appelée delta T (ΔT), influence la quantité de chaleur qui traverse une paroi. Si la température intérieure est de 20°C et qu’il fait -10°C dehors :
ΔT = 20−(−10) = 30 degrés celsius (soit 30 kelvins, noté 30 K).
La puissance thermique (P) nécessaire pour maintenir cette température est :
P = U × S × ΔT
- P : puissance en watts (W)
- U : coefficient de transmission thermique en W/(m²·K)
- S : surface de la paroi en m²
- ΔT : différence de température en kelvins (K)
Exemple : Pour une surface de murs isolés de 100 m² :
Calcul de l’énergie consommée
Sur une période de chauffage de 17 heures l’énergie consommée sera égale à :
E = P×t
- E : énergie en wattheures (Wh)
- P : puissance en watts (W)
- t : temps en heures (h)
E = 600×17 = 10 200 Wh = 10,2 kWh
Estimation du coût de consommation
Avec un tarif électrique de 0,25 €/kWh le coût de cette consommation d’énergie :
Coût = 10,2 × 0,25 = 2,55 €
Conclusion :
Les liens entre l’isolation, la puissance nécessaire pour chauffer un bâtiment et la consommation d’énergie sont plus simples qu’on ne le pense. En comprenant les principes de base et en effectuant quelques calculs, il est possible d’estimer l’impact de l’isolation sur nos factures énergétiques. Une bonne isolation est donc essentielle pour réduire notre consommation d’énergie, faire des économies et contribuer à la protection de l’environnement.